In applications in the physical sciences it is often the case that one does not have the analytic form of the function. In this quite common situation one cannot obtain the coefficients in as straightforward a manner as was done above with the function sin(x). In many cases, one has only a finite set of values and wishes to infer the function. Now, the Taylor series representation quite clearly indicates that in principle one needs all derivatives and so there is not enough information to `completely' construct the function. One must deal with the fact that the best one can do is to find a 'good' approximation to the function. With the Taylor expansion one is assuming that the function is as smooth as needed. This is an assumption which is very often a good assumption in the context of scientific applications. but it is worth noting that it is a separate assumption.
There are some simple functions for which truncating the Taylor series after a given number of terms does not lead to errors in the approximation of the function by the truncated series. Here we record a few of these, as they will arise again in our discussion of numerical derivative approximations. First, consider the linear function
![]()
This function has a straight line graph with slope b. Following the same procedure as with sin(x) we conclude that
![]()
All derivatives higher than the first exactly vanish for this linear function. Thus
the Taylor series representation for ![]() is in fact exact. Also, recall
from elementary algebra that to find the intercept and slope of a straight line one needs
only x and f(x) at two points, which is to say that a straight line can be fit with
just two points.
is in fact exact. Also, recall
from elementary algebra that to find the intercept and slope of a straight line one needs
only x and f(x) at two points, which is to say that a straight line can be fit with
just two points.
Secondly, consider the quadratic function
![]()
All derivatives of this function higher than the second are zero. This means that the Taylor series for the quadratic function terminates after the third term. It then follows that

Hence for the quadratic function the Taylor series expansion is an exact
representation. Only three points are needed to find the three coefficients
in the Taylor expansion. This is also consistent with the idea that only three
points are needed to uniquely pass through a quadratic function. From the fact that
the different terms in the Taylor expansion are directly proportional to the derivatives
of the function evaluated at the given base point ![]() , we see that the three values
needed to fix the quadratic function are determined by the zeroth, first, and second
derivatives.
, we see that the three values
needed to fix the quadratic function are determined by the zeroth, first, and second
derivatives.
Next let us briefly consider the situation which arises when we attempt to approximate
a function with a finite number of terms in its Taylor expansion. We have just seen that
if the function is exactly linear or exactly quadratic, then there is no difference between
the functions and their Taylor series representations. But when the underlying function
is not linear or quadratic the move to represent the function with a linear or a quadratic
or a cubic polynomial is bound to generate errors. Here we will quote the result giving the
truncation error committed when truncating the series at a given term. Let ![]() be the polynomialof order n which results when only n terms are included:
be the polynomialof order n which results when only n terms are included:
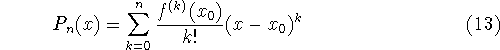
Next, define the remainder ![]() to be
to be
![]()
Then
![]()
In the definition of ![]() , the parameter c is some point between
, the parameter c is some point between ![]() and x.
and x.
![]() represents the truncation error made by chopping off the infinte series to a
series with only n terms. Note that the truncation error is proportional to the
(n+1)st derivative of the (often) unknown function. In many science applications one
does not know the function to begin with, so explicitly evaluating the truncation error
is not feasible. In any event, this result shows that if the function is smooth then the
error made by excluding higher order terms may rapidly decrease as the order of the
approximating polynomial increases.
represents the truncation error made by chopping off the infinte series to a
series with only n terms. Note that the truncation error is proportional to the
(n+1)st derivative of the (often) unknown function. In many science applications one
does not know the function to begin with, so explicitly evaluating the truncation error
is not feasible. In any event, this result shows that if the function is smooth then the
error made by excluding higher order terms may rapidly decrease as the order of the
approximating polynomial increases.
We mention here in passing that the truncation error just discussed is one kind of error which arises from the insistence (or maybe necessity) of representing a function by a finite polynomial. However, there is another source of error called the roundoff error which must be included in any assessment of success or failure of an attempted representation. Roundoff effor arises from the fact that real numbers can be represented by a finite number of bits in a computer and that when arithmetic operations such as multiplication are carried out some accuracy in the product is lost. This is due to the way in which multiplication is performed among two real numbers. Every time a multiplication is performed and the result stored in some location, there are some bits which are 'lost' or become uncertain. We shall have more to say about this source of error later on. For now just keep in mind that this other source of error must be dealt with as well.