G. Comer Duncan - Philip A. Hughes - Mark A. Miller
Jets of goober peas will be shot at relativistic speeds. God only knows what will happen. Give us an infinite amount of resources so we can find out...
Over the last decade the quantity and quality of images of extragalactic relativistic jets have increased to a point where it has become evident that curvature of light-year-scale flows is the norm, not the exception (e.g., Wardle et al. 1994). Some of this curvature may be `apparent', resulting from a more modestly curved flow seen close to the line of sight. Nevertheless, such flows must posses some intrinsic curvature, and thus their 3-D morphology must be addressed.
This raises both questions and possibilities: how can highly relativistic flows suffer significant curvature, and yet retain their integrity? It has been argued (Begelman, Blandford & Rees 1984) that sublight-year-scale flows are highly dissipative, and should radiate a significant fraction of their flow energy if subjected to a perturbation such as bending. How do transverse shocks propagate along a curved flow? Will the shock plane rotate with respect to the flow axis; will the shock strengthen or weaken? What role does flow curvature have to play in explaining phenomena such as stationary knots between which superluminal components propagate (Shaffer et al. 1987), knots which brighten after an initial fading (Mutel et al. 1990), and changing component speed (Lobanov & Zensus 1996). Numerous lines of evidence point convincingly to the occurrence of oblique shocks (e.g., Heinz & Begelman 1997; Lister & Marscher 1999; Marscher et al. 1997; Polatidis & Wilkinson 1998); how do they form and evolve? All these issues are amenable to study through hydrodynamic simulation - but all demand that such simulations be 3-D.
Furthermore, it has become evident over the last five years that such highly energetic flows are also found in Galactic objects with stellar mass `engines'. In the galactic superluminals GRS 1915+105 (Mirabel & Rodríguez 1994, 1995) and GRO J1655-40 (Hjellming & Rupen 1995; Tingay et al. 1995) the observed motions indicate jet flow speeds up to 92%c. There is compelling evidence from the observation of optical afterglow that gamma-ray bursts are of cosmological origin, and whether produced by the mergers of compact objects, or accretion induced collapse (AIC), simple relativistic fireball models seem ruled out, the data strongly favoring highly relativistic jets (Dar 1998). Thus a detailed understanding of the dynamics of collimated relativistic flows has wide application in astrophysics.
This grant application requests resources to perform an initial exploration of the key issues pertaining to the uniquely 3D dynamics of relativistic astrophysical flows.
Since 1993 we have used machines at OSC and elsewhere in a continuing project to study the dynamics and radiation properties of relativistic extragalactic jets. Our first results (Duncan & Hughes 1994) constituted the first-published high-resolution axisymmetric simulations of these objects. That work demonstrated the stability of highly relativistic flows, and suggested an interpretation of a long-known difference between two classes of astrophysical flows in terms of flow speed-dependent stability. That work was performed on a combination of computers, including workstations at BGSU, the University of Michigan, and the OSC Cray and OVL Onyx machines. In addition, OSC personnel helped us make movies of the 2D simulations which proved very useful in both the assessment of the science and the communication of the work.
Some representative graphics illustrating the jet dynamics is shown in the following figures.
That work has subsequently developed along four parallel tracks:
The major focus of the present proposal for OSC resources is the 3D relativistic jet simulations using our Adaptive Mesh Refinement code. Over the last two years we have performed numerous tests on the code and have endeavored to make it as efficient as the underlying algorithms permit. Following this extensive development and testing, the code is ready to be used to perform research level simulations on the OSC Cray T94 and the Origin 2000. The computational requirements of such simulations are significant in both memory and wall clock hours, and the 3D simulations requested herein require facilities of the caliber of those at the OSC, principally due to the memory requirements. The fast, large memory machines such as the Cray T94 and the Origin 2000 are ideal for our purpose, because currently available workstations provide insufficient memory for us to achieve anything like adequate resolution while, as noted in §3.4.2, the use of massively parallel technology still presents serious challenges to AMR-type codes.
The following is a list of specific projects to be done along with estimates of the number of RU needed for each part. These estimates are based on testing done on the OSC Origin 2000 and on the NCSA Origin 2000 cluster.
Specifically, this project plans to
The total requested RU for the project is thus: 1850 RU.
The total number of runs from all four parts of the proposed studies amounts to of the order of ten, with the exact number determined in part by earlier results: novel initial results might compel us to invest more time in few high resolution runs, or a broader exploration of parameter space. Either way, trial runs on the Origin 2000s at both OSC and NCSA provide us with a dependable estimate of the resources required.
We note the very important point that because of our use of Adaptive Mesh Refinement, low resolution 3D runs can be made on workstation class machines with 128Mb of memory. Such runs have insufficient resolution to address the questions set out above, but provide invaluable insight into which initial conditions and parts of parameter space are most appropriate choices for production runs at OSC. We thus expect to need little or no experimentation, and will make efficient use of OSC facilities.
Runs will require typically 1 - 2 Gb of memory (which is available through a
queue - Q95.2g36000 - set up at our request in October 1998). Figure-N
shows the results of an exploratory run with a precessing jet; this required
0.7 Gb on the Origin 2000, and employs 2 levels of refinement on a base grid
of size ![]() . Although interesting, and indeed capable of
giving insight into the dynamics of the flow, the resolution is clearly
insufficient. An additional level of refinement alone would lead to
untenable memory requirements, but an additional level in conjunction with
more selective refinement criteria - restricting refinement to key portions
of the flow - would increase the memory required by no more than
. Although interesting, and indeed capable of
giving insight into the dynamics of the flow, the resolution is clearly
insufficient. An additional level of refinement alone would lead to
untenable memory requirements, but an additional level in conjunction with
more selective refinement criteria - restricting refinement to key portions
of the flow - would increase the memory required by no more than ![]() .
.
Our current calculations assume an inviscid and compressible gas, and an
ideal equation of state with constant adiabatic index. We use a Godunov-type
solver which is a relativistic generalization of the method due to Harten,
Lax, & Van Leer (1983), and Einfeldt (1988), in which the full solution to
the Riemann problem is approximated by two waves separated by a piecewise
constant state. We evolve mass density R, the three components of the
momentum density ![]() ,
, ![]() and
and ![]() , and the total energy density E
relative to the laboratory frame. Earlier, 2D axisymmetric calculations
computed the axial and radial components of momentum density,
, and the total energy density E
relative to the laboratory frame. Earlier, 2D axisymmetric calculations
computed the axial and radial components of momentum density, ![]() and
and
![]() , in a cylindrical coordinate system.
, in a cylindrical coordinate system.
Defining the vector
![]()
and the three flux vectors
![]()
![]()
![]()
the conservative form of the relativistic Euler equation is
![]()
The pressure is given by the ideal gas equation of state ![]() The Godunov-type solvers are well known
for their capability as robust, conservative flow solvers with excellent
shock capturing features. In this family of solvers one reduces the problem
of updating the components of the vector U, averaged over a cell, to the
computation of fluxes at the cell interfaces. In one spatial dimension the
part of the update due to advection of the vector U may be written as
The Godunov-type solvers are well known
for their capability as robust, conservative flow solvers with excellent
shock capturing features. In this family of solvers one reduces the problem
of updating the components of the vector U, averaged over a cell, to the
computation of fluxes at the cell interfaces. In one spatial dimension the
part of the update due to advection of the vector U may be written as
![]()
In the scheme originally devised by Godunov (1959), a fundamental emphasis is
placed on the strategy of decomposing the problem into many local Riemann
problems, one for each pair of values of ![]() and
and ![]() to yield
values which allow the computation of the local interface fluxes
to yield
values which allow the computation of the local interface fluxes
![]() . In general, an initial discontinuity at
. In general, an initial discontinuity at ![]() due to
due to ![]() and
and ![]() will evolve into four piecewise constant states
separated by three waves. The left-most and right-most waves may be either
shocks or rarefaction waves, while the middle wave is always a contact
discontinuity. The determination of these four piecewise constant states can,
in general, be achieved only by iteratively solving nonlinear equations.
Thus the computation of the fluxes necessitates a step which can be
computationally expensive. For this reason much attention has been given to
approximate, but sufficiently accurate, techniques. One notable method is
that due to Harten, Lax, & Van Leer (1983; HLL), in which the middle wave,
and the two constant states that it separates, are replaced by a single
piecewise constant state. One benefit of this approximation, which smears
the contact discontinuity somewhat, is to eliminate the iterative step, thus
significantly improving efficiency. However, the HLL method requires
accurate estimates of the wave speeds for the left- and right-moving waves.
Einfeldt (1988) analyzed the HLL method and found good estimates for the wave
speeds. The resulting method combining the original HLL method with
Einfeldt's improvements (the HLLE method), has been taken as a starting
point for our simulations. In our implementation we use wave speed estimates
based on a simple application of the relativistic addition of velocities
formula for the individual components of the velocities, and the relativistic
sound speed
will evolve into four piecewise constant states
separated by three waves. The left-most and right-most waves may be either
shocks or rarefaction waves, while the middle wave is always a contact
discontinuity. The determination of these four piecewise constant states can,
in general, be achieved only by iteratively solving nonlinear equations.
Thus the computation of the fluxes necessitates a step which can be
computationally expensive. For this reason much attention has been given to
approximate, but sufficiently accurate, techniques. One notable method is
that due to Harten, Lax, & Van Leer (1983; HLL), in which the middle wave,
and the two constant states that it separates, are replaced by a single
piecewise constant state. One benefit of this approximation, which smears
the contact discontinuity somewhat, is to eliminate the iterative step, thus
significantly improving efficiency. However, the HLL method requires
accurate estimates of the wave speeds for the left- and right-moving waves.
Einfeldt (1988) analyzed the HLL method and found good estimates for the wave
speeds. The resulting method combining the original HLL method with
Einfeldt's improvements (the HLLE method), has been taken as a starting
point for our simulations. In our implementation we use wave speed estimates
based on a simple application of the relativistic addition of velocities
formula for the individual components of the velocities, and the relativistic
sound speed ![]() , assuming that the waves can be decomposed into components
moving perpendicular to the two coordinate directions.
, assuming that the waves can be decomposed into components
moving perpendicular to the two coordinate directions.
In order to compute the pressure p and sound speed ![]() we need the rest
frame mass density n and energy density e. However, these quantities are
nonlinearly coupled to the components of the velocity as well as to the
laboratory frame variables via the Lorentz transformation:
we need the rest
frame mass density n and energy density e. However, these quantities are
nonlinearly coupled to the components of the velocity as well as to the
laboratory frame variables via the Lorentz transformation:
![]()
![]()
![]()
![]()
![]()
where ![]() is the Lorentz factor and
is the Lorentz factor and ![]() . When the adiabatic index is constant it
is possible to reduce the computation of n, e,
. When the adiabatic index is constant it
is possible to reduce the computation of n, e, ![]() ,
, ![]() and
and
![]() to the solution of the following quartic equation:
to the solution of the following quartic equation:
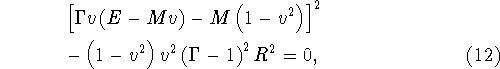
where ![]() . This quartic is solved at
each cell several times during the update of a given mesh using
Newton-Raphson iteration.
. This quartic is solved at
each cell several times during the update of a given mesh using
Newton-Raphson iteration.
Our scheme is generally of second order accuracy, which is achieved by taking the state variables as piecewise linear in each cell, and computing fluxes at the half-time step. However, in estimating the laboratory frame values on each cell boundary, it is possible that through discretization, the lab frame quantities are unphysical - they correspond to rest frame values v;SPMgt;1 or p;SPMlt;0. At each point where a transformation is needed, we check that certain conditions on M/E and R/E are satisfied, and if not, recompute cell interface values in the piecewise constant approximation. We find that such `fall back to first order' rarely occurs.
The relativistic HLLE (RHLLE) method discussed above constitutes the basic flow integration scheme on a single mesh. Our past and planned work also utilizes adaptive mesh refinement (AMR) in order to gain spatial and temporal resolution.
The AMR algorithm used is a general purpose mesh refinement scheme which is
an outgrowth of original work by Berger (1982) and Berger and Colella
(1989). The AMR method uses a hierarchical collection of grids consisting of
embedded meshes to discretize the flow domain. We have used a scheme which
subdivides the domain into logically rectangular meshes with uniform spacing
in the three coordinate directions, and a fixed refinement ratio of ![]() . The AMR algorithm orchestrates i) the flagging of cells which need
further refinement, assembling collections of such cells into meshes; ii) the
construction of boundary zones so that a given mesh is a self-contained
entity consisting of the interior cells and the needed boundary information;
iii) mechanisms for sweeping over all levels of refinement and over each mesh
in a given level to update the physical variables on each such mesh; and iv)
the transfer of data between various meshes in the hierarchy, with the
eventual completed update of all variables on all meshes to the same final
time level. The adaption process is dynamic so that the AMR algorithm places
further resolution where and when it is needed, as well as removing
resolution when it is no longer required. Adaption occurs in time, as well
as in space: the time step on a refined grid is less than that on the coarser
grid, by the refinement factor for the spatial dimension. More time steps are
taken on finer grids, and the advance of the flow solution is synchronized by
interleaving the integrations at different levels. This helps prevent any
interlevel mismatches that could adversely affect the accuracy of the
simulation.
. The AMR algorithm orchestrates i) the flagging of cells which need
further refinement, assembling collections of such cells into meshes; ii) the
construction of boundary zones so that a given mesh is a self-contained
entity consisting of the interior cells and the needed boundary information;
iii) mechanisms for sweeping over all levels of refinement and over each mesh
in a given level to update the physical variables on each such mesh; and iv)
the transfer of data between various meshes in the hierarchy, with the
eventual completed update of all variables on all meshes to the same final
time level. The adaption process is dynamic so that the AMR algorithm places
further resolution where and when it is needed, as well as removing
resolution when it is no longer required. Adaption occurs in time, as well
as in space: the time step on a refined grid is less than that on the coarser
grid, by the refinement factor for the spatial dimension. More time steps are
taken on finer grids, and the advance of the flow solution is synchronized by
interleaving the integrations at different levels. This helps prevent any
interlevel mismatches that could adversely affect the accuracy of the
simulation.
In order for the AMR method to sense where further refinement is needed, some monitoring function is required. We have used a combination of the gradient of the laboratory frame mass density, a test that recognizes the presence of contact surfaces, and a measure of the cell-to-cell shear in the flow, the choice of which functions to use being determined by which part of the flow is of most significance in a given study. Since the tracking of shock waves is of paramount importance, a buffer ensures the flagging of extra cells at the edge of meshes, ensuring that important flow structures do not `leak' out of meshes during the update of the hydrodynamic solution. The combined effect of using the RHLLE single mesh solver and the AMR algorithm results in a very efficient scheme. Where the RHLLE method is unable to give adequate resolution on a single coarse mesh the AMR algorithm places more cells, resulting in an excellent overall coverage of the computational domain.
Our current calculations assume an inviscid and compressible gas, and an
ideal equation of state with constant adiabatic index. We use a Godunov-type
solver which is a relativistic generalization of the method due to Harten,
Lax, & Van Leer (1983), and Einfeldt (1988), in which the full solution to
the Riemann problem is approximated by two waves separated by a piecewise
constant state. We evolve mass density R, the three components of the
momentum density ![]() ,
, ![]() and
and ![]() , and the total energy density E
relative to the laboratory frame. Earlier, 2D axisymmetric calculations
computed the axial and radial components of momentum density,
, and the total energy density E
relative to the laboratory frame. Earlier, 2D axisymmetric calculations
computed the axial and radial components of momentum density, ![]() and
and
![]() , in a cylindrical coordinate system.
, in a cylindrical coordinate system.
Defining the vector
![]()
and the three flux vectors
![]()
![]()
![]()
the conservative form of the relativistic Euler equation is
![]()
The pressure is given by the ideal gas equation of state ![]() The Godunov-type solvers are well known
for their capability as robust, conservative flow solvers with excellent
shock capturing features. In this family of solvers one reduces the problem
of updating the components of the vector U, averaged over a cell, to the
computation of fluxes at the cell interfaces. In one spatial dimension the
part of the update due to advection of the vector U may be written as
The Godunov-type solvers are well known
for their capability as robust, conservative flow solvers with excellent
shock capturing features. In this family of solvers one reduces the problem
of updating the components of the vector U, averaged over a cell, to the
computation of fluxes at the cell interfaces. In one spatial dimension the
part of the update due to advection of the vector U may be written as
![]()
In the scheme originally devised by Godunov (1959), a fundamental emphasis is
placed on the strategy of decomposing the problem into many local Riemann
problems, one for each pair of values of ![]() and
and ![]() to yield
values which allow the computation of the local interface fluxes
to yield
values which allow the computation of the local interface fluxes
![]() . In general, an initial discontinuity at
. In general, an initial discontinuity at ![]() due to
due to ![]() and
and ![]() will evolve into four piecewise constant states
separated by three waves. The left-most and right-most waves may be either
shocks or rarefaction waves, while the middle wave is always a contact
discontinuity. The determination of these four piecewise constant states can,
in general, be achieved only by iteratively solving nonlinear equations.
Thus the computation of the fluxes necessitates a step which can be
computationally expensive. For this reason much attention has been given to
approximate, but sufficiently accurate, techniques. One notable method is
that due to Harten, Lax, & Van Leer (1983; HLL), in which the middle wave,
and the two constant states that it separates, are replaced by a single
piecewise constant state. One benefit of this approximation, which smears
the contact discontinuity somewhat, is to eliminate the iterative step, thus
significantly improving efficiency. However, the HLL method requires
accurate estimates of the wave speeds for the left- and right-moving waves.
Einfeldt (1988) analyzed the HLL method and found good estimates for the wave
speeds. The resulting method combining the original HLL method with
Einfeldt's improvements (the HLLE method), has been taken as a starting
point for our simulations. In our implementation we use wave speed estimates
based on a simple application of the relativistic addition of velocities
formula for the individual components of the velocities, and the relativistic
sound speed
will evolve into four piecewise constant states
separated by three waves. The left-most and right-most waves may be either
shocks or rarefaction waves, while the middle wave is always a contact
discontinuity. The determination of these four piecewise constant states can,
in general, be achieved only by iteratively solving nonlinear equations.
Thus the computation of the fluxes necessitates a step which can be
computationally expensive. For this reason much attention has been given to
approximate, but sufficiently accurate, techniques. One notable method is
that due to Harten, Lax, & Van Leer (1983; HLL), in which the middle wave,
and the two constant states that it separates, are replaced by a single
piecewise constant state. One benefit of this approximation, which smears
the contact discontinuity somewhat, is to eliminate the iterative step, thus
significantly improving efficiency. However, the HLL method requires
accurate estimates of the wave speeds for the left- and right-moving waves.
Einfeldt (1988) analyzed the HLL method and found good estimates for the wave
speeds. The resulting method combining the original HLL method with
Einfeldt's improvements (the HLLE method), has been taken as a starting
point for our simulations. In our implementation we use wave speed estimates
based on a simple application of the relativistic addition of velocities
formula for the individual components of the velocities, and the relativistic
sound speed ![]() , assuming that the waves can be decomposed into components
moving perpendicular to the two coordinate directions.
, assuming that the waves can be decomposed into components
moving perpendicular to the two coordinate directions.
In order to compute the pressure p and sound speed ![]() we need the rest
frame mass density n and energy density e. However, these quantities are
nonlinearly coupled to the components of the velocity as well as to the
laboratory frame variables via the Lorentz transformation:
we need the rest
frame mass density n and energy density e. However, these quantities are
nonlinearly coupled to the components of the velocity as well as to the
laboratory frame variables via the Lorentz transformation:
![]()
![]()
![]()
![]()
![]()
where ![]() is the Lorentz factor and
is the Lorentz factor and ![]() . When the adiabatic index is constant it
is possible to reduce the computation of n, e,
. When the adiabatic index is constant it
is possible to reduce the computation of n, e, ![]() ,
, ![]() and
and
![]() to the solution of the following quartic equation:
to the solution of the following quartic equation:
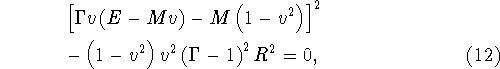
where ![]() . This quartic is solved at
each cell several times during the update of a given mesh using
Newton-Raphson iteration.
. This quartic is solved at
each cell several times during the update of a given mesh using
Newton-Raphson iteration.
Our scheme is generally of second order accuracy, which is achieved by taking the state variables as piecewise linear in each cell, and computing fluxes at the half-time step. However, in estimating the laboratory frame values on each cell boundary, it is possible that through discretization, the lab frame quantities are unphysical - they correspond to rest frame values v;SPMgt;1 or p;SPMlt;0. At each point where a transformation is needed, we check that certain conditions on M/E and R/E are satisfied, and if not, recompute cell interface values in the piecewise constant approximation. We find that such `fall back to first order' rarely occurs.
The relativistic HLLE (RHLLE) method discussed above constitutes the basic flow integration scheme on a single mesh. Our past and planned work also utilizes adaptive mesh refinement (AMR) in order to gain spatial and temporal resolution.
The AMR algorithm used is a general purpose mesh refinement scheme which is
an outgrowth of original work by Berger (1982) and Berger and Colella
(1989). The AMR method uses a hierarchical collection of grids consisting of
embedded meshes to discretize the flow domain. We have used a scheme which
subdivides the domain into logically rectangular meshes with uniform spacing
in the three coordinate directions, and a fixed refinement ratio of ![]() . The AMR algorithm orchestrates i) the flagging of cells which need
further refinement, assembling collections of such cells into meshes; ii) the
construction of boundary zones so that a given mesh is a self-contained
entity consisting of the interior cells and the needed boundary information;
iii) mechanisms for sweeping over all levels of refinement and over each mesh
in a given level to update the physical variables on each such mesh; and iv)
the transfer of data between various meshes in the hierarchy, with the
eventual completed update of all variables on all meshes to the same final
time level. The adaption process is dynamic so that the AMR algorithm places
further resolution where and when it is needed, as well as removing
resolution when it is no longer required. Adaption occurs in time, as well
as in space: the time step on a refined grid is less than that on the coarser
grid, by the refinement factor for the spatial dimension. More time steps are
taken on finer grids, and the advance of the flow solution is synchronized by
interleaving the integrations at different levels. This helps prevent any
interlevel mismatches that could adversely affect the accuracy of the
simulation.
. The AMR algorithm orchestrates i) the flagging of cells which need
further refinement, assembling collections of such cells into meshes; ii) the
construction of boundary zones so that a given mesh is a self-contained
entity consisting of the interior cells and the needed boundary information;
iii) mechanisms for sweeping over all levels of refinement and over each mesh
in a given level to update the physical variables on each such mesh; and iv)
the transfer of data between various meshes in the hierarchy, with the
eventual completed update of all variables on all meshes to the same final
time level. The adaption process is dynamic so that the AMR algorithm places
further resolution where and when it is needed, as well as removing
resolution when it is no longer required. Adaption occurs in time, as well
as in space: the time step on a refined grid is less than that on the coarser
grid, by the refinement factor for the spatial dimension. More time steps are
taken on finer grids, and the advance of the flow solution is synchronized by
interleaving the integrations at different levels. This helps prevent any
interlevel mismatches that could adversely affect the accuracy of the
simulation.
In order for the AMR method to sense where further refinement is needed, some monitoring function is required. We have used a combination of the gradient of the laboratory frame mass density, a test that recognizes the presence of contact surfaces, and a measure of the cell-to-cell shear in the flow, the choice of which functions to use being determined by which part of the flow is of most significance in a given study. Since the tracking of shock waves is of paramount importance, a buffer ensures the flagging of extra cells at the edge of meshes, ensuring that important flow structures do not `leak' out of meshes during the update of the hydrodynamic solution. The combined effect of using the RHLLE single mesh solver and the AMR algorithm results in a very efficient scheme. Where the RHLLE method is unable to give adequate resolution on a single coarse mesh the AMR algorithm places more cells, resulting in an excellent overall coverage of the computational domain.
While there exist many implementations of distributed Adaptive Mesh Refinement in 3D (e.g. DAGH, PYRAMID), the problems associated with implementing an efficient method remain largely unsolved. Specifically, the issues of load balancing and data locality present large obstacles in constructing an efficient AMR implementation in a distributed memory environment. We have based our AMR implementation on a simple Fortran 90 derived data type. We plan to eventually employ multiple processor technology at two different levels. First, we plan to utilize recent advances in High Performance Fortran (HPF) compiler technology in our code. This will enable us to access distributed memory architectures. Second, we plan to implement the shared memory parallelism offered by the SGI Origin 2000.
Code compilation has been performed with extensive but safe optimization (typically -O2). We have avoided certain options (e.g., the -OPT:IEEE_ arithmetic=3 option of the Origin 2000) to minimize potential rounding error induced problems. The code makes few calls to intrinsic math functions and performs no standard tasks such as linear equation solving or fast Fourier transformation. We have thus not called upon libraries with optimized functions or packages.
Profiling has been used to very good effect: in an early version of the code profiling revealed that interpolation to populate newly generated grids - in particular to provide boundary values during advance of the solution to a common time on all grid levels - took 58.5% of the processor time. Recoding to perform this interpolation on a grid-by-grid, rather than point-by-point basis reduced the time spent in this task to 6.5% in a fiducial problem, with 77% of the time spent on core calculations pertaining to the calculation of fluxes and updating conserved variables.
perfex data from a run on the Origin 2000 - a machine well-suited to the current project - showed a graduated instructions per cycle value of 0.78, somewhat, but not substantially, below 1.0. Graduated loads (and stores) per issued loads (and stores) were close to 1.0; both L1 and L2 data cache hit rates were above 0.93. In general, perfex indicates that the code suffers no significant inefficiencies.